Benford’s
Law and Fair Value Accounting
DRAFT
THIS
DRAFT SHOULD NOT BE RELIED UPON FOR ACADEMIC, SCIENTIFIC, LEGAL OR OTHER USES.
THIS DRAFT CONSISTS OF UNVETTED, UNVERIFIED STATEMENTS THAT COULD CHANGE AT ANY
TIME.
Yigal Rechtman 2007-2008©
The issuance of Financial Accounting Standard No. 157 “Fair Value Measurement” has been hailed as the ‘final frontier’ of the convergence of US GAAP with International Financial Reporting Standards (IFRS). FAS 157 adequately defines the various estimation models that accountants may use for fair value balances, including some new concepts based on market participation and recognition rules. However, the Financial Accounting Standards Board in issuing FAS 157 indirectly accepts that - barring the availability of independent pricing of “active markets” - valuation techniques are based on assumptions and judgment (FAS 157, ¶18-19). Accordingly, although a fair value hierarchy is promulgated as a standard (FAS 157, ¶21) absent an active market in assets or liabilities, a fair value estimation model is required for measurement and recognition of balances.
Fair value accounting is a concept that accountants have grappled with mostly because it does not fit neatly with the historic cost accounting paradigm. For most accountants measurement of historic cost makes sense because it is “objective and verifiable”; Fair-value measurement and even recognition has been criticized by some as neither objective nor verifiable.
The fair-value paradigm is at times criticized for being heavily reliant on valuation estimation models which can be viewed as subjective or bias. For valuation purposes, a model is created by the entity recognizing a balance in its financial report. The balance is a result of an application of the model on a set of values with a fixed and known set of assumptions that limits the values – either explicitly or implicitly. We can imagine any model used for estimation as a water dam used to generate electricity: water arrives at fluctuating rates of speed and quantity towards a dam. The dam operator applies pre-set rules for opening or closing gates, based on the fluctuation of the water. As a result a body of water is accumulated at the lake in front of the dam and the gates allow final and objective amount and controlled of water to escape through them to the electric plant.
In the fair value accounting model, the stream of historical values is analogous to the water arriving towards the dam; the valuation model itself is the set of gates and rules that are applied to the aggregate in-coming stream of values. Certain in-coming values are excluded (held in a “lake”) by applying rules and assumptions of what are acceptable input values. These filtering assumptions are analogous to the pre-set rules of how the dam should be operated. The resulting balance in a fair-value model is analogous to the final strength and quantity of the water allowed to leave the dam. The dam-operator uses a set of constant and known rules and assumptions, to create an even flow out of the dam. This would be similar to selecting certain calculations and methods as the acceptable ones within the fair-value estimation model. The ultimate objective from a fair-value perspective is an least-biased final value which can be tested for validity with minimal judgment calls.
An example for an estimation model would be the use of a simple average to arrive at a final balance. Suppose an accountant is out to obtain the fair-value measurement of accounts receivable, net of an allowance for doubtful accounts. The question before her is as follows: how to measure accounts receivable and the off-setting balance (represented by a contra-account) in order to properly recognize the “real” fair value of the account at year-end. In the historic cost paradigm, the accountant can use historical cost information which is often based on subsequent events that were not known exactly at a period’s end but are known subsequently to it. However, in the fair value paradigm, the accounting is not simply done close to the year-end but is at times projected to future periods for which such hind-sight is not possible. Suppose then, that she wishes to know the fair value of accounts receivable without knowing a-priori the events and rate of collections subsequent to the period’s end. What would be the model utilized? The fair-value paradigm (the “dam”) would take prior experiences of accounts receivable values (stream of “water”) and apply specific rules (“gates”) and assumptions to them to arrive at a final balance. The accountant could use an estimation model such as an average of prior periods that contain an implicit assumption such as an equal-weight for each value (or a weighted-average, in a more sophisticated model). The result of the application of the estimation model is a single value which can be said to be the fair value of accounts receivable without having the benefits of any hind-sight knowledge.
Of course, the claim that fair value accounting is neither objective nor verifiable is evident from the example above. If the accountant would use a method weighted averages, there is a real possibility that weights (assumptions) will be used incorrectly or with a bias. If a simple average of four interim quarters’ would be used to arrive at the rate uncollectible accounts (i.e. uncollectible accounts divided by the balance at the end of each quarter) the implicit and bias assumption would be that all quarters are homogenous. However, if one of the quarters is lump-sided because of some extra-ordinary write off, this assumption would be flawed, limiting the objectivity and reliability of the estimate. Similarly, if a weighted average of four quarters is used, and the weights used do not reflect the level of activity of each quarter, the assumptions again could be flawed as well.
By attempting to estimate a fair-value balance at year-end without any hind-sight knowledge will be by definition an unverifiable balance, at least from the prospective of measuring the real value of the account. No degree of fine-turning will allow the accountant to verify a-priori that the fair-value account balance is in fact the balance. The fair-value accounting model is thus relegated to a mere ‘best estimate’ with an underlying and possibly bias assumption. Same will hold true for balances that are verifiable and objective in the historic cost paradigm such as investments, fixed assets, short and long term liabilities and even revenues or expenses.
What is Benford’s Law?
Benford’s law is a statistical model that is utilized in forensic accounting. It is based on a sufficiently large sample of a ‘naturally occurring’ group of values. ‘Naturally occurring’ values are numbers that can not be assigned but occur within normal operation or measurement. For example, zip codes and area codes are not natural occurring, but phone bills’ balances and the lengths of rivers are naturally occurring. The latter two can not be set in any way, except for the units of measure while the former two are completely arbitrary and their values are based on a composition of two or more random values. For example, the phone bill balance is a composition of random lengths of conversation, at random hours to which a standard set of rates has been applied to.
In the use of Benford’s law the first left-most digit (LMD) or the first two left most digits (2LMD) there is almost invariably a logarithmic scale distribution of values. For example, given a sample of a naturally occurring measurement and you’ll find that the probability of the left most digit being the value “1” is about 30%. The chances of the LMD being “2” are about 15% and the LMD being “3” are about 8% [for more on Benford’s law see side bar]. This statistical phenomenon is intuitive because most measurements begin with the value 1 and go upwards (or downwards in negative numbers). Final mathematical proof of Benford’s law was given in 1995 by T.P. Hill.
The application of Benford’s law is often used by forensic accountants and auditors with respect to fraud. Auditors apply it to a large population of transactions when seeking anomalies in the data. The use of Benford’s law is has been cited in professional circles in connection to auditing and in particular with reference to Statement of Auditing Standards number 99, “Consideration of Fraud in a Financial Statement Audit”.[1]
The application of Benford’s law can also be used in testing the validity of fair value estimates for which hind-sight verifiability and objectivity are at unknown. The application is straight forward and has a single requirement: that the supporting values in the fair-value model will be sufficiently numerous to be considered a sample for Benford’s law use.
In the example given above, the accountant applied a simple average to the last four quarters’ balance of uncollectible accounts to arrive at a net accounts receivable. The fair value model uses a total of four (4) instances and a simple-average model. The assumption is really implicit and can be stated as “the four quarters are equal in importance”. The average of the four quarters yields a single final balance. The sample of a single final balance would be insufficient to be used in a Benford’s law application because it is too small. Accordingly, the fair-value estimation model has to use a more granular set of data with a larger number of values. To accommodate this requirement a different estimation model can be constructed and tested: suppose that the accountant obtains a stream of daily data in a large enough quantity. An example for such data would be the entire transactional details of credit sales. Let’s assume that there are 100,000 such transactions. Practically as well as theoretically, the application of Benford’s law would be more reliable with such a large number of instances, so we will assume we will be using an application of the entire set of credit-sales amounts for the entire year.
The accountant can use a model that produces the ratio of the individual credit sale balance to the gross accounts receivable at the end of the transaction day. The rationale behind this ratio is that accounts receivable is a bucket from which credits (received payments) are drawn and debits (sales) are added, so the daily balance of the account is really a composition of the two opposing directions. The value of the incoming debits is really dependant on the value of the offsetting credits, and to arrive at the fair-value of these transactions, the effect of the off-setting credits is to be considered. The combined daily ratio of 100,000 credit sales transaction can then be used to project on the final balance at year’s end[2].
The transactional estimation model of course, is a more sophisticated a model than a four-quarter’ average described above and some may be reluctant to develop such a model. However, the granularity of the model really provides a greater measure of reliability because it is transactional base, not aggregate based as in the quarterly average model.
Next, the resulting fluctuating ratio that is used to project the fair-value of the account balance (in this example, accounts receivable net of allowance for doubtful accounts) can be tested to ascertain that it falls within the normal logarithmic scale of LMD or 2LMD. The Benford’s law distribution of the ratio of two semi-dependents variables (debits and credits) against the resulting composite balance can provide an objective and verifiable validation of the balance.
The model used in this example is only one valuation model that was assembled by the author for demonstration purposes. Valuation models that de-aggregate balances into transactional activity can be composed for other balances from either the balance sheet or profit and loss accounts. Obviously, the ending balances of balance sheet accounts are more applicable for fair-value accounting. The relationship between these ending balances and the transactional activity on the profit-and-loss accounts is the key to properly utilize a fair-value model to these balances.
Similarly, in the investment area – often cited as a most appropriate for fair-value accounting, the application of a valuation model can be based on historical cost activity of trading or end-of-day balances to project a fair-value balance. The use of Benford’s law on the historical cost detailed activity can provide further comfort that the devised model is less subjective and more verifiable.
The proposed use of Benford’s law requires two additional steps before it could be, as some like to say “admissible in court”. First, more validation of the massive body of empirical but unproven data has to be available with respect to the logarithmic scale that Benford’s law present for left-most-digit values. Secondly and seperatley, research of valuation models that are applicable to Benford’s law validation by utilizing underlying transactional data (versus aggregated balances) should be able to further our understanding of these model’s behavior, validity and possible flaws. Finally, a note about actual application: models based on a transactional level activity are practically possible with the advent and use of data mining and data aggregation technology. Although the validity of the data mining methods is outside the scope of this discussion, it should be noted that the use of technology should be a matter of interest for the fair-value accountant to be familiar with in order to maintain the quality of their fair-value models.
Yigal Rechtman 2007© DRAFT
Not a final copy. Distribution or copy without written permission is prohibited.
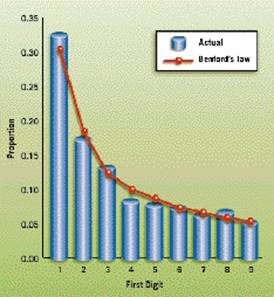
Exhibit 1 shows the results of a LMD analysis of the
population counts of the 3,141
|
Data Sets |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Benford’s Law, expected |
30.1 |
17.6 |
12.4 |
9.6 |
7.9 |
6.6 |
5.7 |
5.1 |
4.5 |
|
Rivers, Area |
31.0 |
16.4 |
10.7 |
11.3 |
7.2 |
8.6 |
5.5 |
4.2 |
5.1 |
|
Population |
33.9 |
20.4 |
14.2 |
8.1 |
7.2 |
6.2 |
4.1 |
3.7 |
2.2 |
|
American League |
32.7 |
17.6 |
12.6 |
9.8 |
7.4 |
6.4 |
4.9 |
5.6 |
3.0 |
|
Reader's Digest |
33.4 |
18.5 |
12.4 |
7.5 |
7.1 |
6.5 |
5.5 |
4.9 |
4.2 |
Exhibit 2 shows various naturally occurring measurements in comparison to Benford’s Law expected results for LMD distribution. Adapted from: www.sciencenews.org, June 27, 1998.
[1] For example, Dirtschi, C. et al, “The Effective Use of Benford’s Law to Assist in Detecting Fraud in Accounting Data”, Journal of Forensic Accounting, Vol V (2004), pp. 17-34
[2] The projection can take places as follows: the average ratio (ignoring sign) of transaction sales to day’s end balance is applied to the total year’s credit sales and payments received. The result is an average daily accounts receivable that is annualized to arrive at a fair value balance of accounts receivable. Any measurement below the historic cost accounts receivable balance can be recognized as an allowance for bad debt expense.